DMesh: A Differentiable Representation for General Meshes

Sanghyun Son¹, Matheus Gadelha², Yang Zhou², Zexiang Xu², Ming C. Lin¹, Yi Zhou²

1. University of Maryland, College Park
2. Adobe Research

(→) Optimization process of DMesh. DMesh defines existence probability of each face in the mesh. Therefore, it can handle mesh of various topology, and change edge connectivity during optimization. We can use DMesh to reconstruct mesh, starting from random state (up) or sample points (down).

Abstract

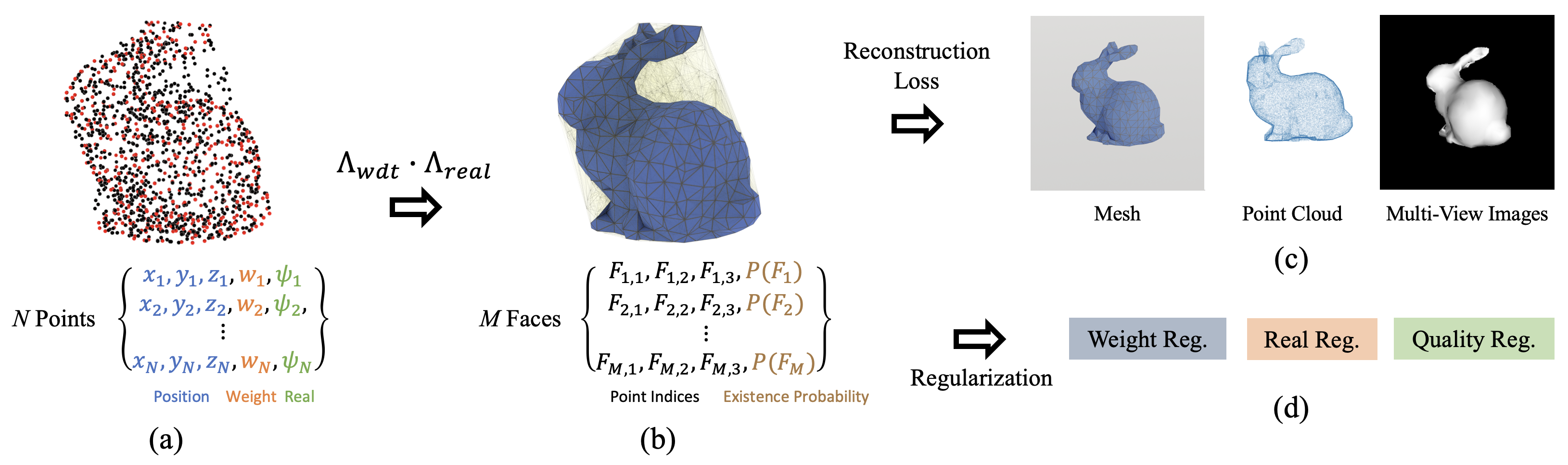
We present a differentiable representation, DMesh, for general 3D triangular meshes. DMesh considers both the geometry and connectivity information of a mesh. In our design, we first get a set of convex tetrahedra that compactly tessellates the domain based on Weighted Delaunay Triangulation (WDT), and formulate probability of faces to exist on our desired mesh in a differentiable manner based on the WDT. This enables DMesh to represent meshes of various topology in a differentiable way, and allows us to reconstruct the mesh under various observations, such as point cloud and multi-view images using gradient-based optimization.

Overview

Overall pipeline of DMesh.

DMesh is an explicit shape representation that encodes every information into point cloud.
Then, we determine existence probability of faces based on the point cloud to extract mesh.
Therefore, we optimize the point attributes to reconstruct the target 3D mesh.

Point cloud of DMesh (Left) and extracted mesh (Right) during optimization.

Point cloud reconstruction (Left) / First (Middle) and last (Right) epoch of multi-view image reconstruction.

DMesh handles mesh connectivity in a differentiable manner.
Therefore, it admits dynamic topology change.

Point cloud reconstruction result for open surface (left), closed surface (middle), and mixed surface (right).

DMesh is very general representation, which can handle closed and open surfaces together.

Experiment: Mesh to DMesh

Since DMesh handles mesh connectivity in a differentiable manner, it can optimize point attributes to recover the ground truth connectivity as much as possible, with only small perturbations to the vertices of the mesh.

Ground truth mesh (Left) and DMesh (Right) during optimization.

Even though there are slight perturbations to the vertex positions, DMesh can restore 99% of connectivity of the ground truth mesh, while only having less than 1% false positive ratio. The periodical flickering of DMesh is induced by additional point insertion.

Experiment: Point Cloud Reconstruction

Here we assume each point cloud is comprised of 100K points. From there, we sample 10K points to initialize DMesh. Then, we optimize DMesh by minimizing the expected Chamfer Distance loss to the given point cloud.

Point cloud of DMesh (Left) and extracted mesh (Right) during optimization.

In the point cloud rendering, the color of each point represents its real value.
Note that some points disappear because they lose weights and thus discarded during optimization.

Extracted mesh without edges (Left) and with edges (Right) during optimization.

Since we already have sample points, we can use their subset to initialize our mesh.
Therefore, it converges fast to the target shape in several optimization steps.
Note that connectivity keeps changing mainly due to additional regularizations.

Effect of point orientations in the mesh reconstruction results.

In our formulation, we can consider point orientations in reconstructing our mesh.
When we give a larger coefficient for the point orientations, the reconstructed mesh usually gave more favorable results (left).
Interestingly, when we set the coefficient to a large value, we could also observe a compact mesh that aligns with geometric features well (right).

Experiment: Multi-view Image Reconstruction

Here we assume that we are given diffuse and depth rendering of ground truth mesh from 64 viewpoints. We use differentiable renderer to render the object, and optimize mesh based on L1 loss to the given images. Unlike point cloud reconstruction, we start optimization from random state, as we do not have sample points. We take a coarse-to-fine approach, and optimize for 4 epochs. At the start of each epoch, we sample points from the previous mesh and use them to initialize the mesh. The number of sample points increase to get better, fine-grained results.

Epoch 1: Start optimization from 8000 regularly distributed points.

Epoch 2: Sample 1000 points from previous mesh to initialize mesh, and optimize.

Epoch 3: Sample 3000 points from previous mesh to initialize mesh, and optimize.

Epoch 4: Sample 10000 points from previous mesh to initialize mesh, and optimize.

BibTeX

@misc{son2024dmesh,
      title={DMesh: A Differentiable Representation for General Meshes}, 
      author={Sanghyun Son and Matheus Gadelha and Yang Zhou and Zexiang Xu and Ming C. Lin and Yi Zhou},
      year={2024},
      eprint={2404.13445},
      archivePrefix={arXiv},
      primaryClass={cs.CV}
}