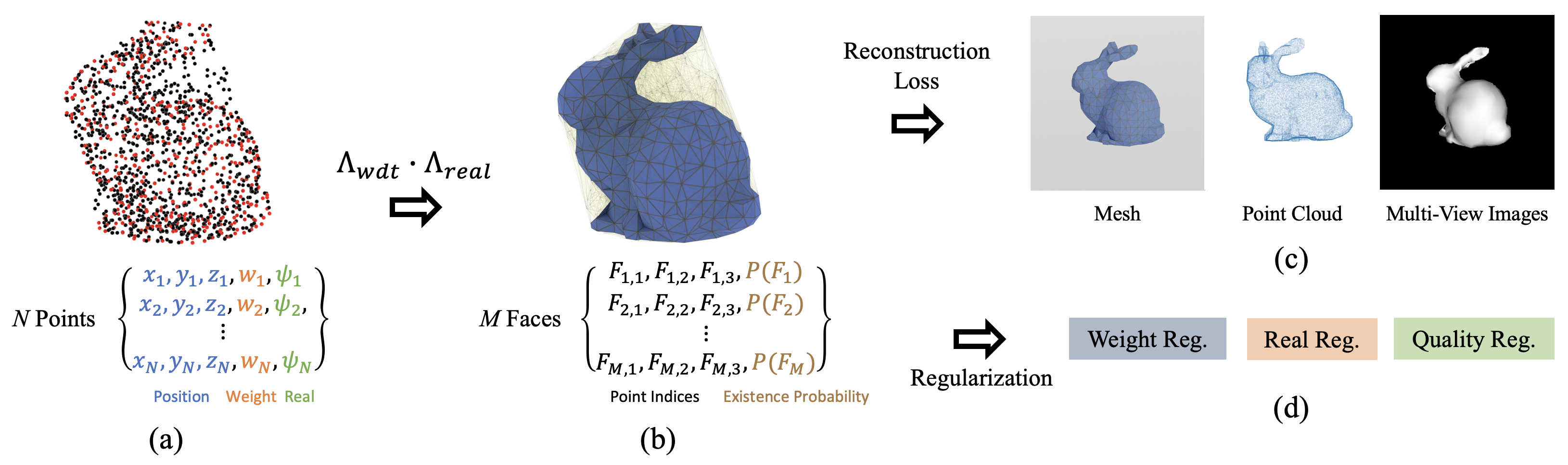
We present a differentiable representation, DMesh, for general 3D triangular meshes. DMesh considers both the geometry and connectivity information of a mesh. In our design, we first get a set of convex tetrahedra that compactly tessellates the domain based on Weighted Delaunay Triangulation (WDT), and formulate probability of faces to exist on our desired mesh in a differentiable manner based on the WDT. This enables DMesh to represent meshes of various topology in a differentiable way, and allows us to reconstruct the mesh under various observations, such as point cloud and multi-view images using gradient-based optimization.